|
|
|
Following Ramanujan ![]() (1913-14), write
(1913-14), write
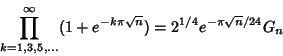 |
(1) |
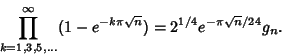 |
(2) |
| (3) | |||
| (4) | |||
| (5) | |||
| (6) |
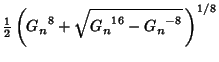 |
(7) | ||
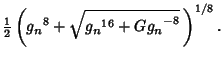 |
(8) |
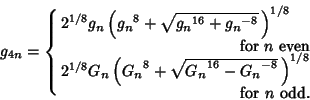 |
(9) |
In terms of the Parameter ![]() and complementary Parameter
and complementary Parameter ![]() ,
,
| (10) | |||
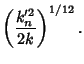 |
(11) |
| (12) |
| (13) |
![$\displaystyle {\textstyle{1\over 2}}[\sqrt{1+{G_n}^{-12}}-\sqrt{1-{G_n}^{-12}}\,]$](r_396.gif) |
(14) | ||
| (15) |
See also G-Function
References
Borwein, J. M. and Borwein, P. B. Pi & the AGM: A Study in Analytic Number Theory and Computational Complexity.
New York: Wiley, pp. 139 and 298, 1987.
Ramanujan, S. ``Modular Equations and Approximations to
![]() .'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
.'' Quart. J. Pure. Appl. Math. 45, 350-372, 1913-1914.
![]() Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
Weisstein, E. W. ``Elliptic Singular Values.'' Mathematica notebook EllipticSingular.m.
|
|
|
© 1996-9 Eric W. Weisstein