The Line Element is
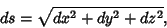 |
(1) |
so the Arc Length between the points 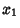 and
and 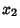 is
is
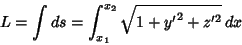 |
(2) |
and the quantity we are minimizing is
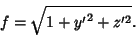 |
(3) |
Finding the derivatives gives
and
so the Euler-Lagrange Differential Equations become
These give
 |
(10) |
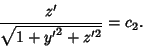 |
(11) |
Taking the ratio,
 |
(12) |
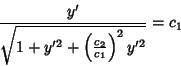 |
(13) |
![\begin{displaymath}
y'^2={c_1}^2\left[{1+y'^2+\left({{c_2\over c_1}}\right)^2 y'^2}\right]= {c_1}^2+y'^2({c_1}^2+{c_2}^2),
\end{displaymath}](p2_916.gif) |
(14) |
which gives
 |
(15) |
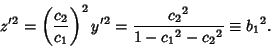 |
(16) |
Therefore,  and
and 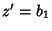 , so the solution is
, so the solution is
![\begin{displaymath}
\left[{\matrix{x\cr y\cr z\cr}}\right]=\left[{\matrix{x\cr a_1x+a_0\cr b_1x+b_0\cr}}\right],
\end{displaymath}](p2_921.gif) |
(17) |
which is the parametric representation of a straight line with parameter
![$x \in [x_1,x_2]$](p2_922.gif) . Verifying the Arc Length gives
. Verifying the Arc Length gives
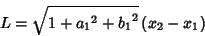 |
(18) |
where
![\begin{displaymath}
\left[{\matrix{y_1\cr y_2\cr}}\right] = \left[{\matrix{x_1 & 1\cr x_2 & 1\cr}}\right]\left[{\matrix{a_1\cr a_0\cr}}\right]
\end{displaymath}](p2_924.gif) |
(19) |
![\begin{displaymath}
\left[{\matrix{z_1\cr z_2\cr}}\right] = \left[{\matrix{x_1 & 1\cr x_2 & 1\cr}}\right]\left[{\matrix{b_1\cr b_0\cr}}\right].
\end{displaymath}](p2_925.gif) |
(20) |
See also Point-Point Distance--1-D, Point-Point Distance--2-D,
Point-Quadratic Distance
© 1996-9 Eric W. Weisstein
1999-05-25

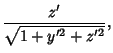


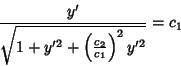
![\begin{displaymath}
y'^2={c_1}^2\left[{1+y'^2+\left({{c_2\over c_1}}\right)^2 y'^2}\right]= {c_1}^2+y'^2({c_1}^2+{c_2}^2),
\end{displaymath}](p2_916.gif)
![\begin{displaymath}
\left[{\matrix{x\cr y\cr z\cr}}\right]=\left[{\matrix{x\cr a_1x+a_0\cr b_1x+b_0\cr}}\right],
\end{displaymath}](p2_921.gif)