|
|
|
The Jacobi elliptic functions are standard forms of Elliptic Functions. The three basic
functions are denoted
![]() ,
,
![]() , and
, and
![]() , where
, where ![]() is known as the Modulus. In terms of Theta Functions,
is known as the Modulus. In terms of Theta Functions,
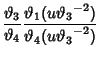 |
(1) | ||
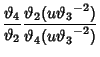 |
(2) | ||
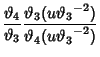 |
(3) |
| (4) |
The Jacobi elliptic functions are periodic in ![]() and
and ![]() as
as
| (5) |
| (6) |
| (7) |
The
![]() ,
,
![]() , and
, and
![]() functions may also be defined as solutions to the differential equations
functions may also be defined as solutions to the differential equations
| (8) |
| (9) |
| (10) |
The standard Jacobi elliptic functions satisfy the identities
| (11) | |||
| (12) | |||
| (13) | |||
| (14) |
| (15) | |||
| (16) | |||
| (17) | |||
| (18) | |||
| (19) |
In terms of integrals,
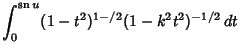 |
(20) | ||
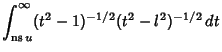 |
(21) | ||
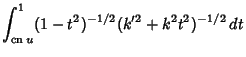 |
(22) | ||
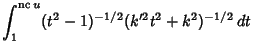 |
(23) | ||
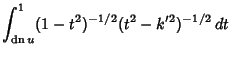 |
(24) | ||
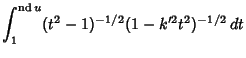 |
(25) | ||
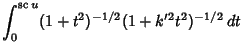 |
(26) | ||
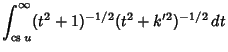 |
(27) | ||
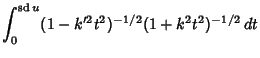 |
(28) | ||
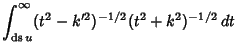 |
(29) | ||
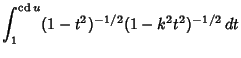 |
(30) | ||
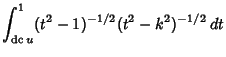 |
(31) |
Jacobi elliptic functions addition formulas include
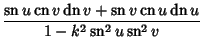 |
(32) | ||
 |
(33) | ||
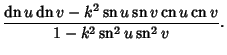 |
(34) |
| (35) | |||
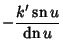 |
(36) | ||
| (37) |
| (38) | |||
| (39) | |||
| (40) |
For Complex arguments,
| (41) |
| (42) |
| (43) |
Derivatives of the Jacobi elliptic functions include
| (44) | |||
| (45) | |||
| (46) |
Double-period formulas involving the Jacobi elliptic functions include
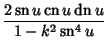 |
(47) | ||
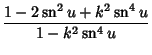 |
(48) | ||
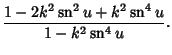 |
(49) |
Half-period formulas involving the Jacobi elliptic functions include
| (50) | |||
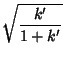 |
(51) | ||
| (52) |
Squared formulas include
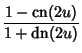 |
(53) | ||
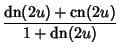 |
(54) | ||
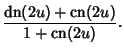 |
(55) |
See also Amplitude, Elliptic Function, Jacobi's Imaginary Transformation, Theta Function, Weierstraß Elliptic Function
References
Abramowitz, M. and Stegun, C. A. (Eds.). ``Jacobian Elliptic Functions and Theta Functions.'' Ch. 16 in
Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, 9th printing.
New York: Dover, pp. 567-581, 1972.
Bellman, R. E. A Brief Introduction to Theta Functions. New York: Holt, Rinehart and Winston, 1961.
Morse, P. M. and Feshbach, H. Methods of Theoretical Physics, Part I. New York: McGraw-Hill, p. 433, 1953.
Press, W. H.; Flannery, B. P.; Teukolsky, S. A.; and Vetterling, W. T.
``Elliptic Integrals and Jacobi Elliptic Functions.'' §6.11 in
Numerical Recipes in FORTRAN: The Art of Scientific Computing, 2nd ed. Cambridge, England:
Cambridge University Press, pp. 254-263, 1992.
Spanier, J. and Oldham, K. B. ``The Jacobian Elliptic Functions.''
Ch. 63 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 635-652, 1987.
Whittaker, E. T. and Watson, G. N. A Course in Modern Analysis, 4th ed. Cambridge, England:
Cambridge University Press, 1990.
|
|
|
© 1996-9 Eric W. Weisstein