|
|
|

A discontinuous ``step'' function, also called the Unit Step, and defined by
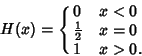 |
(1) |
| (2) |
| (3) |
Bracewell (1965) gives many identities, some of which include the following. Letting ![]() denote the Convolution,
denote the Convolution,
| (4) |
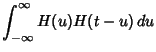 |
(5) | ||
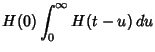 |
|||
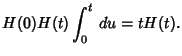 |
(6) |
| (7) |
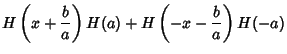 |
|||
 |
(8) |
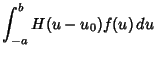 |
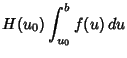 |
(9) | |
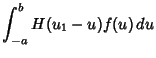 |
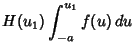 |
(10) |
| (11) |
The Heaviside step function can be defined by the following limits,
![$\displaystyle \lim_{t\to 0}\left[{{\textstyle{1\over 2}}+ {1\over\pi} \tan^{-1}\left({x\over t}\right)}\right]$](h_739.gif) |
(12) | ||
| (13) | |||
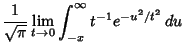 |
(14) | ||
| (15) | |||
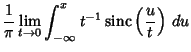 |
(16) | ||
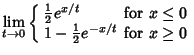 |
(17) | ||
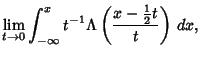 |
(18) |
The Fourier Transform of the Heaviside step function is given by
| (19) |
See also Boxcar Function, Delta Function, Fourier Transform--Heaviside Step Function, Ramp Function, Ramp Function, Rectangle Function, Square Wave
References
Bracewell, R. The Fourier Transform and Its Applications. New York: McGraw-Hill, 1965.
Spanier, J. and Oldham, K. B. ``The Unit-Step
![]() and Related Functions.''
Ch. 8 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 63-69, 1987.
and Related Functions.''
Ch. 8 in An Atlas of Functions. Washington, DC: Hemisphere, pp. 63-69, 1987.
|
|
|
© 1996-9 Eric W. Weisstein