第二章 初等几何图形的计算与作图
几何图形是从现实世界中抽象出来的,所以,几何图形的理论、计算与作图广泛应用与人们的社会实践中.
本章重点介绍两类常用的几何图形:一是平面图形,如三角形、四边形、正多边形以及与圆有关的各种图形;另一是空间立体图形,如正方体、长方体、球体、锥体、圆柱体以及各种正多面体.这里较详细地收集了它们的面积、体积、侧面积、表面积、重心和转动惯量等计算公式.
另外,还介绍了一些图形(如正多边形)的作图方法,对于生产实践中常用的椭圆作图法和圆弧放样法也作了简要的说明.同时,明确指出了在百余年前已经严格证明了的所谓“几何三大问题”不能用尺规作图.
§1 三角形与四边形
一、 三角形各元素的计算
 |
 |
||
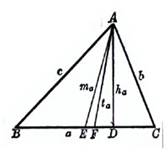
1. 三角形各元素
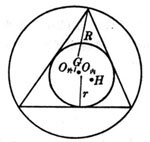
图 2.1 图 2.2
a,b,c为三角形三边 R为外接圆半径
A,B,C为三个角![]() r为内切圆半径
r为内切圆半径
AD![]() 为a边上的高
H为垂心(三条高的交点)
为a边上的高
H为垂心(三条高的交点)
AF![]() 为A角的平分线 G为重心(三条中线的交点)
为A角的平分线 G为重心(三条中线的交点)
AE![]() 为a边上的中线
为a边上的中线
![]() 为内心(三条角平分线的交点)
为内心(三条角平分线的交点)
![]() 为半周长
为半周长![]()
![]() 为外心(三条垂直平分线的交点)
为外心(三条垂直平分线的交点)
S为![]() 的面积
的面积
![]()
2. 三角形各元素计算公式
[高]
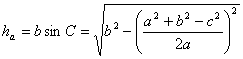
[中线]
![]()
[角分线]
![]()
[面积]
![]()
[外接圆半径]
![]()
[内切圆半径]
![]()
二、 三角形和四边形的面积、几何重心、转动惯量计算公式
|
图形 |
面积S、几何重心G与转动惯量*J |
|
|
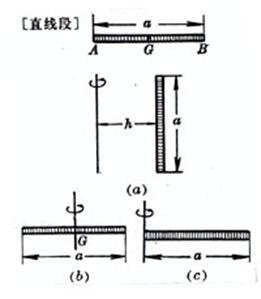
长度 L=a 重心 GA=GB= 转动惯量 (a)转轴平行于细杆,到细杆距离 为h(图(a))
(b)转轴通过细杆重心G,且与细杆 垂直(图(b))
(c) 转轴通过细杆的一个端点,且与细 杆垂直(图(c ))
|
![]() 表中m为物体的质量,物体都为匀质.一般物体的转动惯量计算公式见第六章,
表中m为物体的质量,物体都为匀质.一般物体的转动惯量计算公式见第六章,
§3,五.
|
图形 |
面积S、几何重心G与转动惯量J |
|
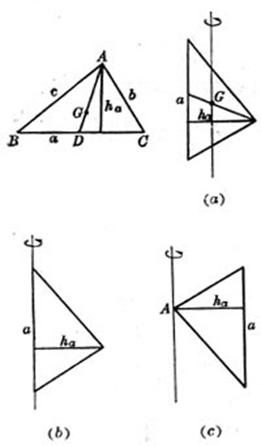
[任意三角形]
a,b,c为三边,
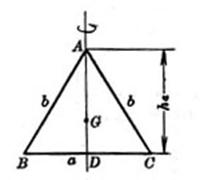
[等腰三角形]
b为两腰,a为底边, |
重心
转动惯量 (a)转轴通过重心G,且与a边平行 (图(a))
(b)转轴与三角形一边a重合(图(b))
(c)转轴通过三角形一顶点A,且平行于a边(图(c ))
重心 转动惯量 转轴与底边上的高
当a=b时
|
|
图形 |
面积S、几何重心G与转动惯量J |
|
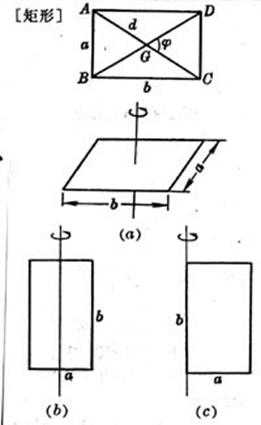
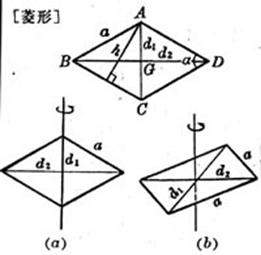
a,b为邻边,d为对角线,
a为边长, |
面积 重心 G在对角线的交点上,即 转动惯量 (a)转轴通过矩形中心,且垂直于矩形所在平面(图(a))
(b)转轴通过矩形中心,且与矩形的b边平行(图(b))
(c)转轴与矩形的b边重合(图(c))
面积 重心G在对角线交点上,即 转动惯量 (a)转轴与对角线
(b)转轴通过重心G且垂直于图形所在平面(图(b))
|
|
图形 |
面积S、几何重心G与转动惯量J |
|
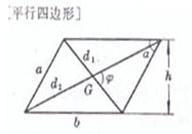
a,b为邻边,h为对边距,
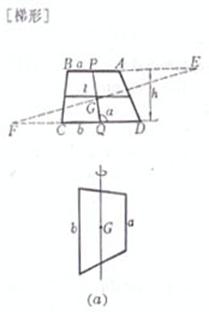
a,b为上下底,h为高,l为两腰中点连线
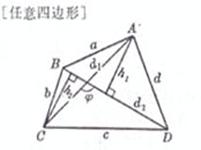
a,b,c,d为四边长, |
面积
重心 G在对角线交点上
面积 重心
转动惯量 转轴通过重心,且平行于上下底 (图(a))
当a=b时(平行四边形)
面积
或
|